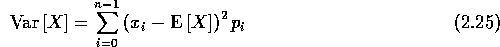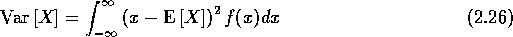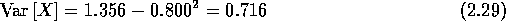Volgende: Standaard deviatie
Terug: Kentallen van een
Vorige: Tweede moment
Een directe toepassing van de misschien nog wat abstracte
grootheid 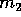 , vinden we, wanneer we van een stochastische
variabele de variantie willen weten. De variantie kan namelijk
direct uitgedrukt worden in het eerste en tweede moment. De
variantie,
, vinden we, wanneer we van een stochastische
variabele de variantie willen weten. De variantie kan namelijk
direct uitgedrukt worden in het eerste en tweede moment. De
variantie, 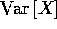 , geeft aan hoe sterk een stochastische
variabele, X, van zijn gemiddelde afwijkt:
, geeft aan hoe sterk een stochastische
variabele, X, van zijn gemiddelde afwijkt:
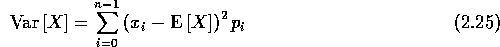
voor een discrete stochastische variabele en
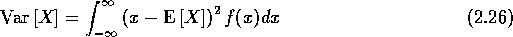
voor een continue stochastische variabele. In beide gevallen
geldt:

ofwel


Stel we willen een maat hebben voor de kwadratische afwijking van
het gemiddelde van het aantal bitfouten in een octet. Deze maat
(de variantie) speelt onder andere een rol als we een
kansverdeling willen benaderen met een Normale verdeling.
Voor de discrete stochastische variabele van het bekende voorbeeld
2.1 berekenen we de variantie met formule (2.27). We kunnen
hierin
de al eerder berekende waarden van het eerste en tweede moment
substitueren. Dit geeft:
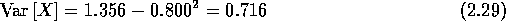
Geert A. Awater
Mon Dec 11 15:33:15 MET 1995
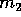 , vinden we, wanneer we van een stochastische
variabele de variantie willen weten. De variantie kan namelijk
direct uitgedrukt worden in het eerste en tweede moment. De
variantie,
, vinden we, wanneer we van een stochastische
variabele de variantie willen weten. De variantie kan namelijk
direct uitgedrukt worden in het eerste en tweede moment. De
variantie, 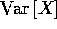 , geeft aan hoe sterk een stochastische
variabele, X, van zijn gemiddelde afwijkt:
, geeft aan hoe sterk een stochastische
variabele, X, van zijn gemiddelde afwijkt: